概述

编译

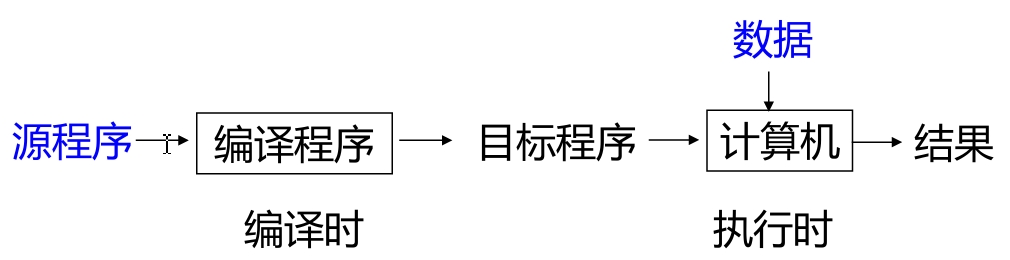
编译：把源程序转换成等价的目标程序的过程即是编译

翻译程序分为两大类：
• 编译程序(即编译器)：把源程序翻译成目标程序的翻译程序
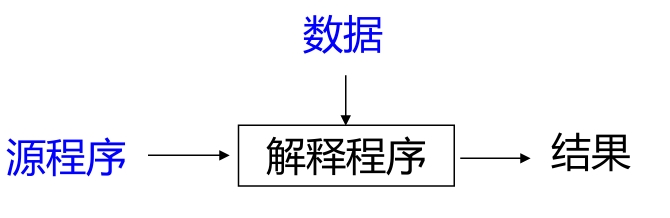
• 解释程序(即解释器)：直接执行源程序的翻译程序

编译程序

两类编译程序：
• 汇编程序
• 编译程序

高级语言程序——编译程序——>低级语言程序
汇编语言程序——汇编程序——>机器语言程序

解释程序

解释程序先将源程序转换成一棵树，遍历该树，执行结点上所规定的动作。

程序语言

程序：本质上说是描述一定数据的处理过程

定义

• 语法：一组规则，用它可以形成和产生一个合式(well-formed)的程序。
• 语义：一组规则，用它可以定义一个程序的意义
• 语用

词法与语法

语法规则和词法规则定义了程序的形式结构

• 词法规则：单词符号的形成规则(单词符号是语言中具有独立意义的最基本结构)
  包括：常数、标识符、基本字、算符、界符等
  描述工具：有限自动机
• 语法规则：语法单位的形成规则
  包括：表达式、语句、分程序、过程、函数、程序等;
  描述工具：上下文无关文法

语义

描述方式

1. 自然语言描述
2. 形式描述
   • 操作语义
   • 指称语义
   • 代数语义

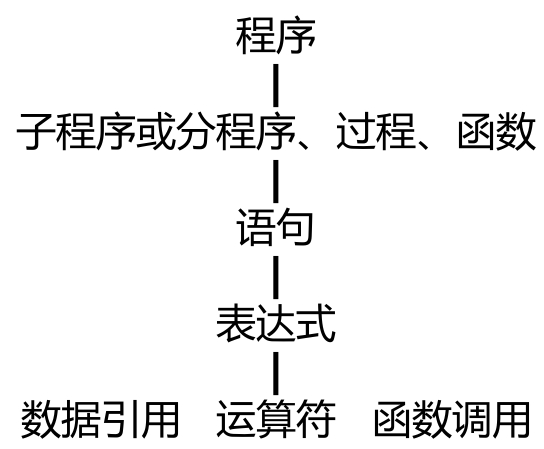
层次

语言特性

作用域

一个名字能被使用的区域范围

名字作用域规则——"最近嵌套原则"

数据类型

三要素

• 属性：用于区别这种类型数据对象的属性
• 值：这种类型的数据对象可以具有的值
• 操作：可以作用于这种类型的数据对象的操作

• 标识符（语法）：以字母开头的，由字母数字组成的字符串
• 名字（语义）：标识程序中的对象

初级数据类型

基本数据类型：

• 数值类型
• 逻辑类型
• 字符类型
• 指针类型

数据结构：

• 数组：逻辑上，数组是由同一类型数据组成的某种n维矩形结构，沿着每一维的距离，称为下标
  内情向量：登记维数，各维的上、下限，首地址，以及数组（元素）的类型等信息
• 记录：由已知类型的数据组合在一起的一种结构
  记录或者结构的元素，也叫做域
• 字符串：符号处理、公式处理
• 表格：本质上是一种记录结构
• 线性表：一组顺序化的记录结构
• 栈：一种线性表，后进先出

抽象数据类型

由数据集合、及其相关的操作组成，这些操作有明确的定义，而且定义不依赖于具体的实现

语句

表达式

• 组成：表达式由运算量（也称操作数，即数据引用或函数调用）和算符（运算符，操作符）组成
• 形式：中缀、前缀、后缀

语句

1. 赋值语句
2. 控制语句
   • 无条件转移语句
   • 循环语句
   • 过程调用语句
   • 条件语句
   • 返回语句

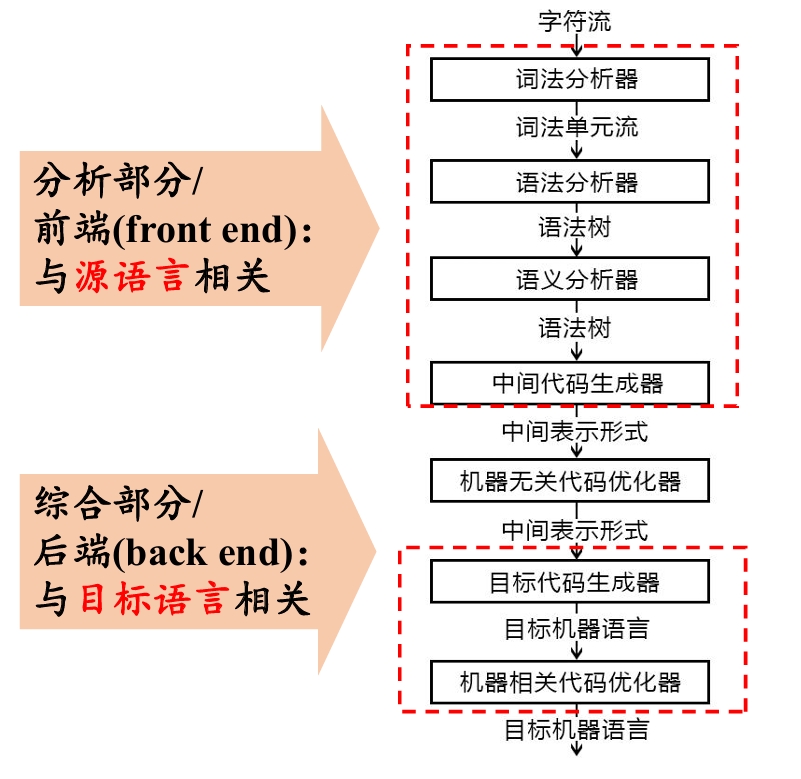
编译器

结构

语法

• 定义：一组规则，用它可以形成和产生一个合式(well-formed)的程序。
• 描述工具：上下文无关文法

数学基础

字母表

概念

字母表∑是一个有穷符号集合

运算

• 字母表∑1和∑2的连接（乘积）定义为：
  ∑1∑2 ={ab|a ∈ ∑1, b ∈ ∑2}
• 字母表∑的n次幂( power)
  ∑0 ={ ε }
  ∑n =∑n-1 ∑ , n ≥ 1
• 字母表∑的正闭包( positive closure)
  ∑+ = ∑ ∪ ∑2 ∪ ∑3 ∪ …
• 字母表∑的克林闭包(Kleene closure)
  ∑* = ∑0 ∪ ∑+ = ∑0 ∪ ∑ ∪ ∑2 ∪ ∑3 ∪ …

串

设∑是一个字母表，对x∈∑*，x称为是∑上的一个串（也叫字）

• 串是字母表中符号的一个有穷序列
• 串s的长度，通常记作|s|，是指s中符号的个数
• 空串是长度为0的串，用 ε（epsilon）表示

运算

• 连接：如果x和y是串，那么x和y的连接(concatenation)是把y附加到x后面而形成的串，记作xy
  空串是连接运算的单位元(identity)，即，对于任何串s都有，εs = sε = s

eg：如果 x=dog且 y=house，那么xy=doghouse

• 幂运算：
  s0= ε，
  sn = sn-1s , n ≥1

eg：如果 s =ba，那么s1= ba，s2=baba，s3=bababa，…

句型和句子

eg：

语言

运算

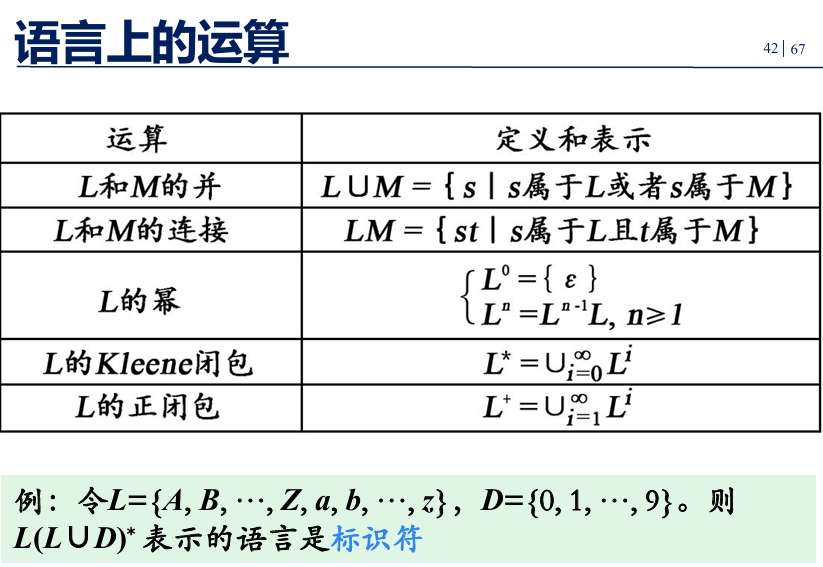
eg：

设文法 G1(A)：A -> c | Ab。G1(A)产生的语言是什么?

推导和归约

• 句子的推导（派生）是从生成语言的角度判定某一词串是否是该语言的句子
• 句子的归约是从识别语言的角度判定某一词串是否是该语言的句子

文法

乔姆斯基于1956年建立形式语言体系，他把文法分成四种类型：0，1，2，3型
它们都由四部分组成，但对产生式的限制有所不同

程序设计语言实际上需要上下文信息（如变量声明、类型检查等），严格来说不属于上下文无关语言（CFG）或上下文有关语言（CSG），但编译器仍主要用CFG描述语法结构，因为CFG解析高效且工具成熟，而上下文相关的约束（如语义规则）则通过符号表和多阶段分析（如语义分析）来补充验证。

0型文法（PSG）

1型文法（CSG）

2型文法（CFG）

语法分析树

分析树是推导的图形化表示

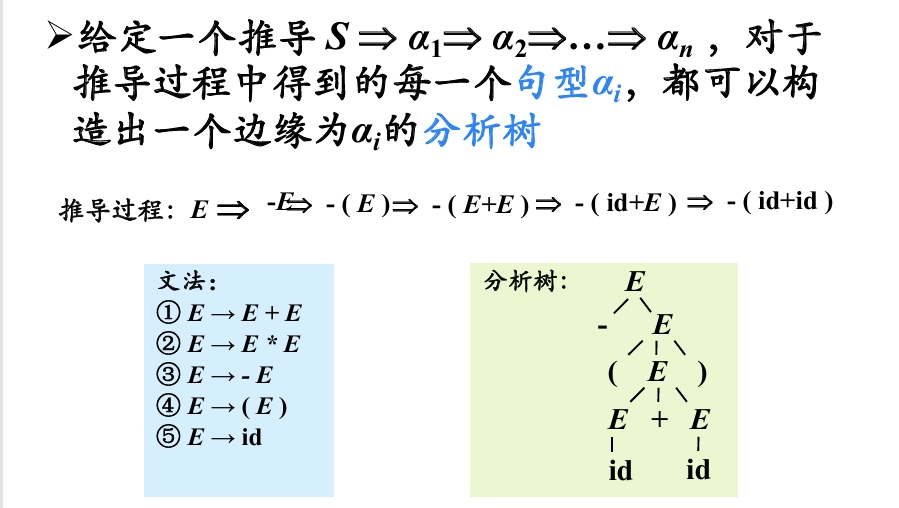
二义性

对于任意一个上下文无关文法，不存在一个算法，判定它是无二义性的；但能给出一组充分条件，满足这组充分条件的文法是无二义性的
eg： G(E): E → i | E + E | E * E | (E)
考虑表达式：i + i * i
它可以被解析成两种不同的结构：

(1) 第一种解析方式（乘法优先）

        E
      / | \
     E  *  E
    /|\    |
   E + E   i
   |   |
   i   i

计算顺序：(i + i) * i（先算加法，再算乘法）

(2) 第二种解析方式（加法优先）

        E
      / | \
     E  +  E
    |    / | \
    i   E  *  E
        |     |
        i     i

计算顺序：i + (i * i)（先算乘法，再算加法）

3型文法（RG）

四种文法比较

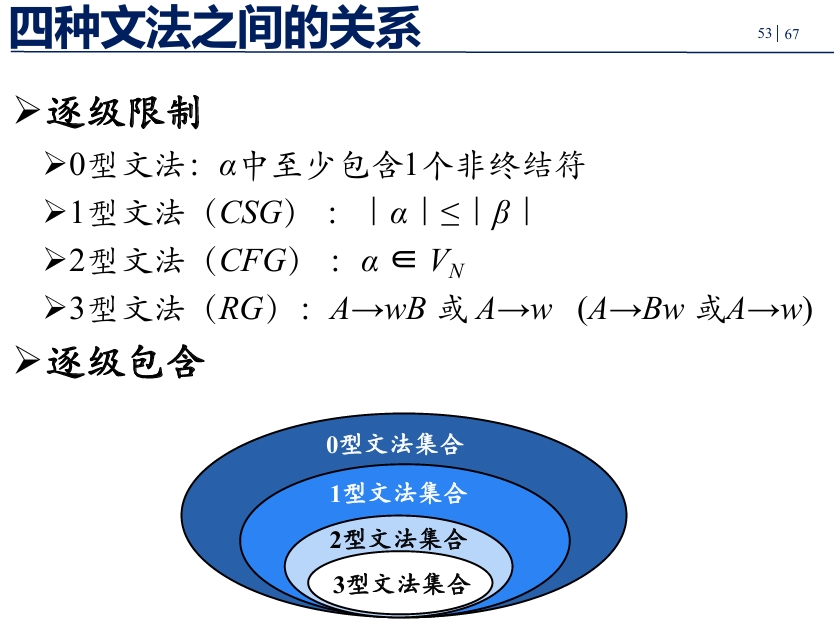
eg：

语法分析

• 目的：在词法分析的基础上，根据语法规则把单词符号串分解成各类语法单位(语法范畴)

语法分析器

从词法分析器输出的token序列中识别出各类短语，并构造语法分析树(parse tree)

词法

• 定义：一组规则，用于将源代码字符流分解为有意义的词法单元（Token），作为语法分析的基本输入单位。
• 描述工具：有限（穷）自动机

词法分析

目的：从左至右逐个字符地对源程序进行扫描，产生一个个单词符号

一些概念：基本字、保留字、标识符、算符、界符

数学基础

正规式

定义

1. 字母表（Σ）

• 一个有限的符号集合（例如 Σ = {a, b}）。

2. 正规集（Regular Set）

• 定义：字母表 Σ 上的正规集是通过以下规则递归构造的字符串集合：
• 基础情况：
  • 空集 ∅ 是正规集。
  • 空串 {ε} 是正规集。
  • 对任意 a ∈ Σ，单字符集 {a} 是正规集。
• 闭合操作（若 A 和 B 是正规集，则以下也是正规集）：
  • 并集：A ∪ B。
  • 连接积：AB = {xy | x ∈ A, y ∈ B}。
  • Kleene 闭包：A* = {ε} ∪ A ∪ AA ∪ AAA ∪ ...。

3. 正规式（Regular Expression）

• 定义：表示正规集的语法表达式，其形式规则如下：
• 基础符号：
  • ∅ 表示空集。
  • ε 表示 {ε}。
  • 对任意 a ∈ Σ，符号 a 表示 {a}。
• 复合表达式（若 e₁ 和 e₂ 是正规式，则以下也是正规式）：
  • 选择：e₁|e₂ 表示 L(e₁) ∪ L(e₂)。
  • 连接：e₁e₂ 表示 L(e₁)L(e₂)。
  • 闭包：e₁* 表示 (L(e₁))*

等价性

若两个正规式表示的正规集相同，则称它们等价。例如：
b(ab)* = (ba)*b。

• 等价律（代数性质）：
• 交换律：e1|e2 = e2|e1
• 结合律：
  • e1|(e2|e3) = (e1|e2)|e3
  • e1(e2e3) = (e1e2)e3
• 分配律：
  • e1(e2|e3) = e1e2 | e1e3
  • (e2|e3)e1 = e2e1 | e3e1
• 单位元：eξ = ξe = e
• 注意：连接运算不满足交换律（即 e1e2 ≠ e2e1）。

词法分析器

执行词法分析的程序

结构

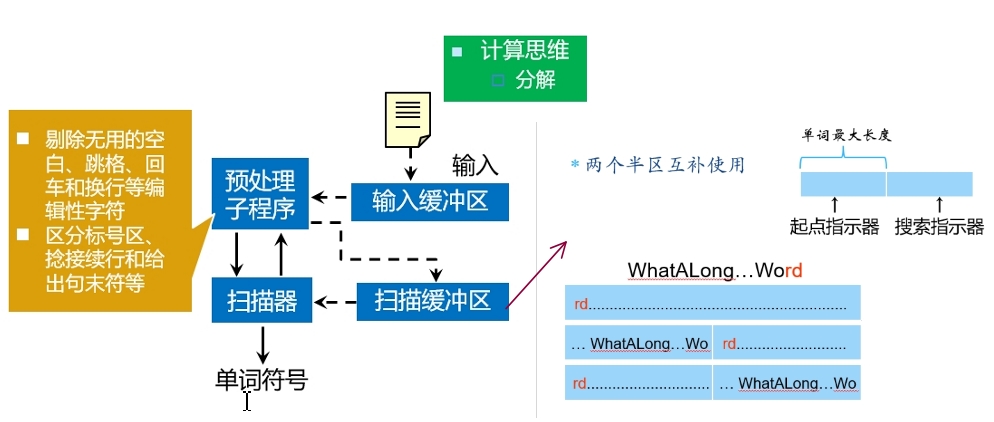
状态转换图

状态转换图是一张有限方向图

• 结点代表状态，用圆圈表示
• 状态之间用箭弧连结，箭弧上的标记(字符)代表射出结点状态下可能出现的输入字符或字符类
• 一张转换图只包含有限个状态，其中有一个为初态，至少要有一个终态
• 每个状态结点对应一小段程序
• 若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于α，则称α被该状态转换图所识别(接受)

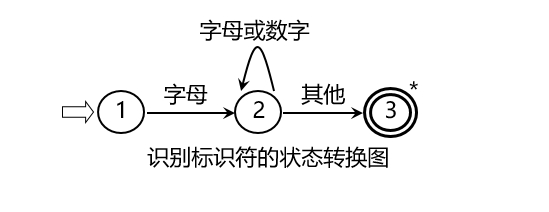
• 状态转换图通过if-else或switch-case作为分支实现，用while作为循环实现，用return作为终态实现。

有限自动机

1. 基本概念
   有穷自动机（FA）是一种抽象的计算模型，用于描述对输入符号串进行处理的系统。它具有以下特点：

   • 有限状态：系统内部状态的数量是有限的。
   • 离散输入：处理的是符号串（如 a, b, 0, 1 等），按顺序逐个读取。
   • 无记忆性：系统的行为仅取决于当前状态和当前输入符号，与历史输入无关。

   eg：FA 类似于一个简单的自动售货机，它根据当前状态（如“等待投币”）和输入（如“投币5元”）决定下一步动作（如“出货”或“显示余额”）。

---

2. 核心组成
   一个FA由以下三部分组成：

   • 输入带（Input Tape）
     • 存储输入符号串（如 aabba），符号来自字母表 Σ。
     • 只读且单向移动：读头从左向右扫描，不能回退或修改输入。
   • 读头（Head）
     • 每次读取一个符号，并向右移动一格。
   • 有穷控制器（Finite Control）
     • 包含有限个内部状态（如 q₀, q₁, q₂）。
     • 根据当前状态和当前输入符号决定下一个状态（通过状态转换规则）。

---

3. 表示方法：转换图（Transition Graph）
   FA 可以用有向图直观表示：

   • 结点：表示状态（如 q₀）。
   • 初始状态：用 start 箭头指向的结点（通常为 q₀）。
   • 终止状态（接收状态）：用双圈标记的结点（如 q₂）。
   • 有向边：若输入 a 使状态从 p 转移到 q，则画边 p → q 并标记 a。

---

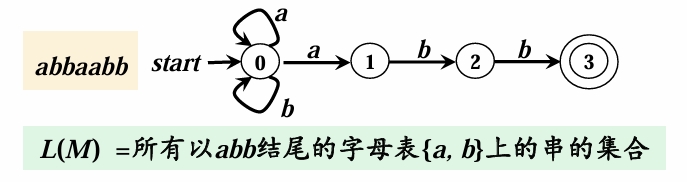
4. FA 的语言
   • 接收（Accept）：若输入串 x 能使FA从初始状态转移到某个终止状态，则 x 被接收。
   • 语言 L(M)：FA定义或接收的所有串的集合。例如：L(M) = {所有以 "ab" 结尾的字符串}。
   • 最长匹配原则：如果输入串的多个前缀均匹配，FA 会选择最长的可接受前缀（如词法分析中识别关键字 if 而非标识符 i）。

---

5. 分类
   FA 分为两类，主要区别在于状态转移的确定性：

类型	DFA（确定的有穷自动机）	NFA（非确定的有穷自动机）
状态转移	每个状态+输入对应唯一的下一个状态。	同一状态+输入可能对应多个下一个状态。
空转移（ε）	不允许。	允许（无需输入即可跳转状态）。
表达能力	与NFA等价，但状态数可能更多。	更灵活，但需转换为DFA实现。

对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价

---

6. 与图灵机的对比

特性	有穷自动机（FA）	图灵机（TM）
存储能力	无外部存储，仅依赖有限状态。	拥有无限长的纸带，可读写和移动。
计算能力	仅能识别正规语言（如正则表达式）。	能识别递归可枚举语言（解决更复杂问题）。
应用场景	词法分析、简单模式匹配。	通用计算（理论上可模拟任何算法）。

---

确定有限自动机(DFA)

1. DFA 的形式化定义

DFA 是一个五元组 M=(S,Σ,f,S₀,F)，其中：

• S：有穷的状态集合（如 {q₀,q₁,q₂）。
• Σ：有穷的输入字母表（如 {a,b}）。
• f：状态转换函数：S×Σ→S，是一个单值映射（确定性关键）。
  • 表示：'f(s,a)=s′ 意为“当前状态 s 遇到输入 a 时，转移到状态 s′”。
• S₀：唯一的初始状态（S₀∈S）。
• F：终止状态集（F⊆S，可为空）。

关键点：DFA 的转换函数 f 必须对每个(s,a) 组合给出唯一确定的下一个状态。

---

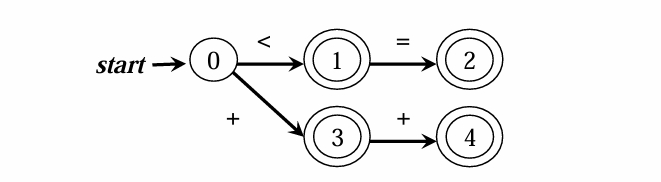
2. DFA 的图形表示（状态转换图）

• 结点：表示状态（如 q₀,q₁）。
• 边：若f(q_i,a)=q_j，则画有向边 q_i——a——>q_j
• 约束：
  • 每个状态结点最多射出∣Σ∣ 条边（每条对应一个输入符号）。
  • 每条边的标记必须来自Σ 且互不相同（保证确定性）。

---

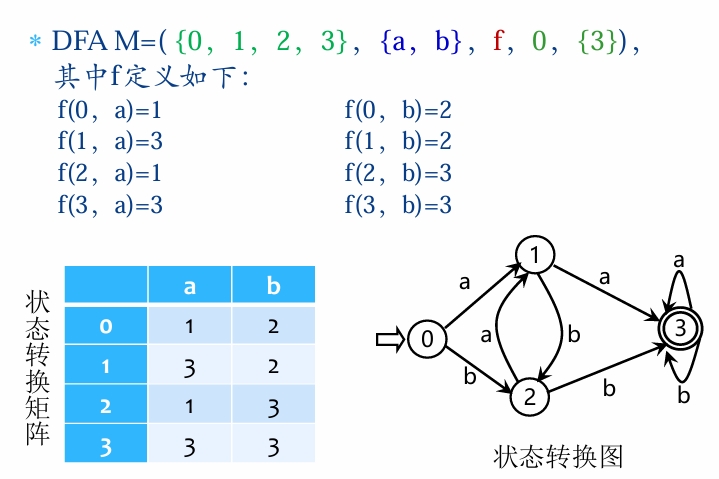
3. DFA 的语言接收

• 接收条件：对输入串 α∈Σ^∗，若存在一条从S₀ 到某个 q^f∈F 的路径，且路径上的标记连接等于α*，则 α* 被 DFA 接收。
• 语言 L*(*M)：DFA M 接收的所有串的集合。
  • 例如：L(M)={α∣α 含偶数个 a}。

---

4. DFA 的特性

   1. 确定性：
      • 每个状态+输入符号的组合唯一确定下一个状态（无歧义）。
      • 无空转移（ε 边）。
   2. 有限性：
      • 状态数和输入符号数均有限，适合计算机实现。
   3. 等价性：
      • 任何 NFA 可通过子集构造法转换为等价的 DFA（但状态数可能指数级增长）

非确定有限自动机(NFA)

1. NFA 的形式化定义

NFA 是一个五元组 M=(S,Σ,f,S₀,F)，其中：

• S：有穷的状态集合（如 {q₀,q₁,q₂）。
• Σ：有穷的输入字母表（如 {a,b}）。
• f：状态转换函数：S×Σ^*→2^s的部分映射
• S₀∈S：非空初态集
• F：终止状态集（F⊆S，可为空）。

关键点：

• NFA可以有多个初态
• 同一个字可能出现在同状态射出的多条弧上
• 弧上的标记可以是Σ*中的一个字(甚至可以是一个正规式)，而不一定是单个字符

2. NFA 的语言接收
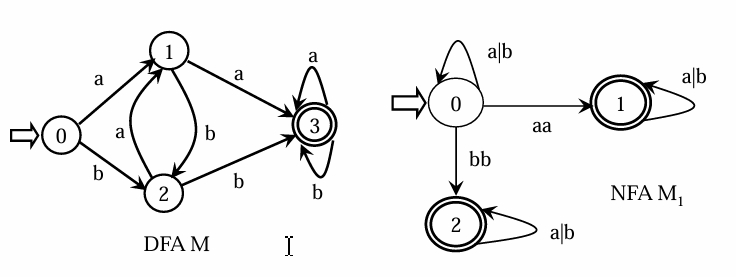
   对于Σ*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记字连接成的字等于α(忽略那些标记为ξ的弧)，则称α为NFAM所识别(接收)。NFAM所识别的字的全体记为L(M)